Optimierung - IMK Engineering – Ingenieurbüro für Mechatronik und Kybernetik Dr. Bruns
Hauptmenü:
Kompetenzen
Kompetenzen ⇒ Optimierung
Die Fachgebiete Optimierung und Operations Research sind einander sehr ähnlich, da in beiden Gebieten nahezu dieselben mathematischen Verfahren zum Einsatz kommen. Wenn es darum geht, technische Systeme oder Prozesse zu optimieren oder deren Parameter zu identifizieren, dann wird zumeist von Optimierung gesprochen. Stehen wirtschaftliche Überlegungen oder die Optimierung betriebswirtschaftlicher Prozesse im Vordergrund, so ist häufig von Operations Research die Rede.
Im Folgenden wird anhand ausgewählter Beispiele gezeigt, wo der Einsatz mathematischer Optimierungsverfahren in Verbindung mit technischen Systemen oder Prozessen sinnvoll und angezeigt ist.
Beispiele:
Bild 1: Numerische, nichtlineare Optimierung mit einem Gradientenverfahren
Identifizierung bzw. Identifikation von Parametern
Wie in den Rubriken Modellbildung & Simulation sowie Regelungstechnik erläutert, ist für den sachgerechten und zielführenden Entwurf einer Regelung ein mathematisches Modell des zu regelnden technischen Systems oder Prozesses zwingend erforderlich. Anderenfalls können sowohl die Auswahl des Regelungsverfahrens als auch die Bestimmung seiner Parameter nur nach dem „Trial-and-Error“-Prinzip erfolgen, dessen negative Implikationen offensichtlich sein sollten.
Ein mathematisches Modell entspricht i.d.R. einem Differentialgleichungssystem, das auf Basis physikalischer Gesetzmäßigkeiten abgeleitet wird. Lineare, gewöhnliche Differentialgleichungssysteme werden für die regelungstechnische Verarbeitung häufig in die sogenannte Zustandsraumdarstellung überführt.
Zustandsraumdarstellung
\[\underline {\dot x} = \underline A \cdot \underline x + \underline B \cdot \underline u \]
Nachdem ein mathematisches Modell mit hoffentlich korrekter Modellstruktur und adäquater Modellierungstiefe (s. a. Modellbildung & Simulation) vorliegt, ist in der Regel jedoch immer noch kein Entwurf der Regelung möglich, da zuvor die Modellparameter korrekt bestimmt werden müssen. Soll bspw. eine Lagereglung für eine über ein Feder-Dämpfer-Element angekoppelte Masse entworfen werden, so ist bei linearem Verhalten die zugehörige Differentialgleichung mit den Parametern $m$ (Masse), $c$ (Federsteifigkeit) und $d$ (Dämpfungskonstante) schnell aufgestellt, die Abbildung des für den Reglerentwurf benötigten dynamischen Verhaltens ergibt sich jedoch letztlich erst aus der konkreten Spezifikation der Parameter $m$ [kg], $c$ [N/m] und $d$ [N/(m/s)]. Manchmal sind alle Parameter bekannt oder können gemessen werden. Was aber, wenn eine Messung fehlender Parameter nicht möglich oder zu aufwändig bzw. zu teuer ist?
Feder-Dämpfer-Element mit angekoppelter Masse
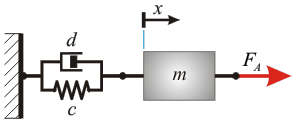
Abgeleitete Differentialgleichung (2. Ordnung)
\[m\ddot x = \sum {F = {F_A}} - d\dot x - cx\]
Zustandsraumdarstellung
für die Analyse im Zeitbereich
\[ \left[ \begin{matrix} \dot x \\ \ddot x \\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 1 \\ -\frac{c}{m} & -\frac{d}{m} \\ \end{matrix} \right] \cdot \left[ \begin{matrix} x \\ \dot x \\ \end{matrix} \right] + \left[ \begin{matrix} 0 \\ \frac{1}{m} \\ \end{matrix} \right] \cdot F_A \]
Übertragungsfunktion (nach LAPLACE)
für die Analyse im Frequenzbereich
\[G\left( s \right) = \frac{{{x}\left( s \right)}}{{{F_A}\left( s \right)}} = \frac{\frac{1}{c}}{{\frac{m}{c}{s^2} + \frac{d}{c}s + 1}}\]
In diesem Fall kann durch Messreihen am realen System, in Kombination mit dem mathematischen Modell und einem geeigneten Optimierungsverfahren, eine Identifizierung bzw. Identifikation der unbekannten Parameter erfolgen. Dazu ist das reale System definiert anzuregen bzw. zu stimulieren (Systemeingang). Gleichzeitig ist die Systemantwort messtechnisch zu erfassen (Systemausgang). Im obigen Beispiel des „Einmassenschwingers“ (Masse $m$, die über ein Feder-Dämpfer-Element angekoppelt ist) wäre eine definierte Anregung bspw. die sprungförmige Beaufschlagung mit einer bekannten Kraft $F_A$ zum Zeitpunkt $t$ (Sprunganregung). Wenn parallel zum zeitlichen Verlauf der anregenden Kraft $F_A$ die Position $x$ der Masse $m$ gemessen wird (Systemantwort), dann können die gesuchten Parameter beispielsweise gemäß der untenstehenden Methodik identifiziert werden.
- Das mathematische Modell bzw. das Simulationsmodell wird mit derselben Anregungsfunktion stimuliert wie das reale System.
- Die Antwort des Simulationsmodells wird mit der gemessenen Antwort des realen Systems verglichen. Dabei wird ein Fehlermaß berechnet, das den Grad der Übereinstimmung von Modellantwort und Systemantwort bewertet. Dieses Fehlermaß kann beispielsweise aus der quadratischen Fehlerfläche zwischen den zeitlichen Verläufen von Modell- und Systemantwort bestehen, muss aber nicht. Auch Fehlermaß-Berechnungen im Frequenzbereich sind häufig sinnvoll und auch angezeigt (siehe Video 2 am Ende der Seite).
- Die Parameter des Modells werden variiert, und es wird wieder zu Schritt 1 übergegangen bzw. eine neue Iteration gestartet. Ziel ist die Minimierung (Optimierung) des Fehlermaßes. Je geringer das Fehlermaß, desto besser wird das reale System durch das Modell beschrieben. Kann das Fehlermaß nicht mehr weiter minimiert werden, so werden der Prozess abgebrochen und weitere Iterationen gestoppt.
Systematik des Optimierungsprozesses
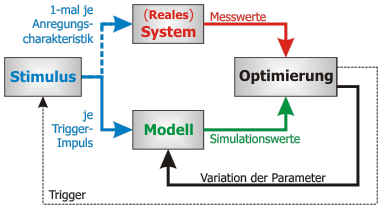
Der zuvor in 3 Schritten beschriebene Prozess kann durch den Einsatz geeigneter Optimierungsverfahren automatisiert werden. In der Regel kommen dabei numerische Verfahren aus dem Bereich der nichtlinearen (und beschränkten) Optimierung zum Einsatz. Dies sind zumeist sogenannte Gradientenverfahren. Sie werden häufig auch als Abstiegsverfahren bezeichnet, da sie Zielfunktionsparameter gemäß dem größten negativen Gradienten (steilster Abstieg, siehe Bild 1) verändern, um möglichst schnell zu einem Minimum zu gelangen. Bezogen auf das obige Beispiel (Einmassenschwinger) wird die Zielfunktion durch den Algorithmus der Fehlermaß-Berechnung repräsentiert. Wie im nebenstehenden Bild skizziert, kann das Fehlermaß dann beispielsweise durch die Fehlerfläche zwischen dem Verlauf einer charakteristischen Systemgröße (Verlauf der Messgröße) und dem Verlauf der entsprechenden Simulationsgröße gemäß dem mathematischen Modell berechnet werden. Das Optimierungsverfahren lenkt alle Parameter ($m$, $c$ und $d$) leicht aus, berechnet den Gradienten aufgrund der Auswirkung auf den Zielfunktionswert, legt eine Schrittweite fest (Veränderung der Parameter) und startet dann mit den neuen Parameterwerten eine neue Iterationsschleife.
Beispiel für eine Ziel- bzw. Fehlerfunktion (im Zeitbereich)
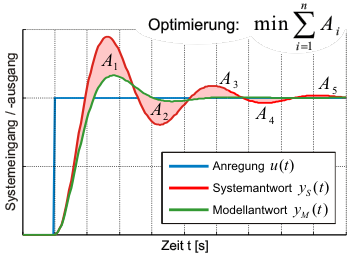
Das folgende Video 1 zeigt eine automatische Parameter-Identifizierung auf Basis eines speziellen Gradientenverfahrens. Bei dem zu identifizierenden System handelt es sich um eine elektrische Reihenschaltung von Widerstand $R$, Induktivität $L$ und Kapazität $C$. Das mathematische Modell ist schnell anhand der KIRCHHOFF’schen Maschenregel abgeleitet. Man erhält eine lineare Differentialgleichung 2. Ordnung. Der Widerstand $R$ ist bekannt. In dem Video ist der Prozess dargestellt, wie die unbekannten Parameter $L$ und $C$ automatisch identifiziert bzw. bestimmt werden.
RLC-Glied

KIRCHHOFF'sche Maschengleichung
${u_E} = {u_R} + {u_L} + {u_C}$, mit ${u_C} = {u_A}$
Abgeleitete Differentialgleichung 2. Ordnung
$${u_E} = Ri + L\frac{{di}}{{dt}} + \frac{1}{C}\int {i\;dt}$$
Das RLC-Glied kann im LAPLACE-Bereich als Übertragungsfunktion und normiert als regelungstechnisches Verzögerungsglied 2. Ordnung darstellt werden. Die Parameter dieser Normalform bestehen dann aus der Verstärkung $K$, der Zeitkonstante $T$ und der (schwingungshemmenden) Dämpfung $D$.
LAPLACE-Transformation des RLC-Glieds (Frequenzbereich)
\[{u_E}\left( s \right) = i\left( s \right)\left( {R + Ls + \frac{1}{{Cs}}} \right),\;\;\;{u_C}\left( s \right) = \frac{1}{{Cs}}i\left( s \right)\]
Übertragungsfunktion 2. Ordnung in regelungstechnischer Normalform
\[G\left( s \right) = \frac{{y\left( s \right)}}{{u\left( s \right)}} = \frac{K}{{{T^2}{s^2} + 2DTs + 1}}\]
Übertragungsfunktion des RLC-Glieds
\[G\left( s \right) = \frac{{{u_A}\left( s \right)}}{{{u_E}\left( s \right)}} = \frac{1}{{LC{s^2} + RCs + 1}}\]
Überbestimmtheit
Ein Koeffizienten-Vergleich bei den zuvor dargestellten Übertragungsfunktionen zeigt, dass den 2 Parametern $T$ und $D$ der Normalform die 3 Parameter $R$, $L$ und $C$ des mathematischen Modells gegenüberstehen, was zu einer „Überbestimmtheit“ des Identifikationsproblems führt! Hier ist große Vorsicht geboten, denn es gibt mehrere Parameterkonfigurationen, die zwar das aktuelle Optimierungsproblem lösen, generell aber zu falschen Modellen führen und somit in anderen Kontexten auch zu falschen Ergebnissen. Im Beispiel des RLC-Glieds muss also mindestens ein Parameter gemessen werden bzw. bekannt sein. Im Video 1 wird der Fall gezeigt, in dem $R$ gemessen wurde und die Parameter $L$ und $C$ im Rahmen einer gradientenbasierten Optimierung automatisch bestimmt wurden.
Die generelle Systematik dieser Optimierung (Video 1) entspricht derjenigen, die beim obigen Beispiel des Einmassenschwingers bereits beschrieben wurde: Das reale System wurde mit einem Spannungssprung angeregt, parallel wurde die (verrauschte) Systemantwort gemessen. Das mathematische Modell wird im Rahmen einer Simulation mit derselben Anregung stimuliert, und die Modell-Parameter werden solange variiert, bis eine bestmögliche Übereinstimmung von gemessener Systemantwort und simulierter Modellantwort erzielt wird.
Lokale Extrema
Bei Video 1 fällt ferner auf, dass die Variation der Parameter nicht strikt in Richtung des steilsten Abstiegs (siehe Bild 1) erfolgt, sondern dass zum Teil große Sprünge auftreten. Der Grund dafür besteht in einer bewussten Modifikation des ursprünglichen Gradientenverfahrens, mit dem Ziel, das „Steckenbleiben“ in einem lokalen Minimum möglichst zu vermeiden. Wie Bild 1 (Startpunkt B) anschaulich zeigt, kann der Optimierungsprozess sehr leicht auch in ein lokales Minimum laufen und dort abbrechen. Dies ist ein weiteres Problem, aber auch hier gibt es adäquate Gegenmaßnahmen.
Hohe Anzahl von Parametern und/oder mehrere Zielfunktionen
Generell nimmt die mit der Optimierung verbundene Problematik zu mit der Anzahl der Parameter einerseits und mit der Anzahl der Zielfunktionen (Mehrzieloptimierung) andererseits. Je mehr Parameter vorhanden sind, desto länger und schwieriger gestaltet sich der Optimierungsprozess. Dem kann man bspw. durch Parameter-Klassifikation und Durchführung einer Sensitivitätsanalyse entgegenwirken. Auch hat sich gezeigt, dass eine Optimierung im Frequenzbereich (Video 2) in der Regel hier zu deutlich besseren Ergebnissen und vor allem kürzeren Optimierungszeiten führt.
Bei mehreren Zielfunktionen ($n>1$) gelangt man automatisch an Punkte (Parameter-Sätze), von denen aus man nicht mehr alle $n$ Zielfunktionswerte gleichzeitig verbessern kann. Man kann dann nur noch $x$ Zielfunktionen ($x>n$) verbessern, während sich $n-x$ Zielfunktionswerte gleichzeitig verschlechtern. Diese Punkte werden als Pareto-Punkte bzw. Pareto-Optima bezeichnet. Auch hier gibt es viele Ansätze und Methoden, wie man „geschickt“ auf Pareto-Mengen „wandert“, um das System (situationsspezifisch) stets im „optimalen“ Zustand zu halten.
Im Hinblick auf die Anwendung von Optimierungsverfahren sind am IMK hohe Kompetenz und langjährige Erfahrung vorhanden. Beispielsweise wurden entsprechende Verfahren im Rahmen des Kreuzungsmanagements [1] und der Fahrwerkentwicklung [2] erfolgreich angewendet.
[1] | Neuendorf, Norbert; Bruns, Torsten: The Multi-Objective Optimiser MOPO in the Decentralised, Autonomous Intersection Management of Vehicles. In: 12th Mediterranean Conference on Control and Automation (Med 2004). Kusadasi, 2004 | |
[2] | Bruns, Torsten; Schäfer, Erika: Modelling and Identification of an All-Terrain Vehicle. International Journal of Vehicle Systems Modelling and Testing, Vol. 2, No. 3, 2007 | |
Um Informationen über den Einsatz von Optimierungsverfahren im Hinblick auf eine Verbesserung der Regelgüte zu erhalten, nutzen Sie bitte den nebenstehenden Link:
Weiter zu Optimierung des geregelten Systems