Regelungstechnik - IMK Engineering – Ingenieurbüro für Mechatronik und Kybernetik Dr. Bruns
Hauptmenü:
Kompetenzen
Kompetenzen ⇒ Regelungstechnik
Die Regelungstechnik stellt Methoden und Algorithmen zur Verfügung, mit denen dynamische Systeme – im Rahmen der Regelungstechnik auch „Regelstrecke“ oder einfach nur „Strecke“ genannt – prinzipiell in gewünschter Weise beeinflusst und somit auch kontrolliert werden können. Voraussetzung dafür ist allerdings, dass über eine sogenannte „Sensorik“ (Sensoren, Messgeräte etc.) Größen erfasst werden können, die den aktuellen Zustand des dynamischen Systems ausreichend genau beschreiben. Der aktuelle Zustand wird dann mit dem gewünschten Soll-Zustand verglichen. Bei erkannten Abweichungen wird durch den „Regler“ korrigierend in das System eingegriffen. Der Systemeingriff erfolgt dabei über die sogenannte „Aktorik“, die auch als „Stellglied“ oder „Stelleinrichtung“ bezeichnet wird. Bei mechatronischen Systemen entspricht der Systemeingriff stets einem Einprägen von Kräften und/oder Momenten in ein mechanisches Grundsystem (Strecke), bspw. durch einen Elektromotor oder einen hydraulischen Aktor.
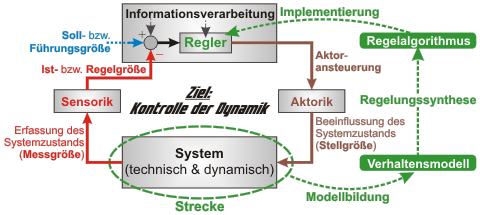
Bild 1: Prozess (grün) der Realisierung von Regelungen
Um einen Regler korrekt auszulegen, wird stets ein physikalisch-mathematisches Modell (Verhaltensmodell) des zu regelnden Systems bzw. der Strecke benötigt, zumindest im Rahmen der am weitesten verbreiteten „linearen Regelungstechnik“. Ohne valides Modell bleibt nur das aufwändige „Trial-and-Error“-Verfahren am realen System für die Auswahl der Reglerstruktur und die Bestimmung der Reglerparameter. Dies führt allerdings zu schlechten bis suboptimalen Ergebnissen und setzt darüber hinaus das System erhöhten Risiken aus, bis hin zur Zerstörung einzelner Komponenten. Am IMK wird deshalb (bei linearen oder linearisierbaren Systemen) stets gemäß der in Bild 1 skizzierten Schritte vorgegangen:
- Modellbildung $\rightarrow$ Verhaltensmodell
- Regelungssynthese $\rightarrow$ Regelalgorithmus
- Reglerimplementierung $\rightarrow$ Regler
Entsprechend der Eigenschaften des Streckenmodells für die Beschreibung des realen Systems lässt sich die Regelungstechnik in die zwei, im Folgenden näher beschriebenen Hauptgebiete „Lineare Regelungstechnik“ und „Nichtlineare Regelungstechnik“ untergliedern.
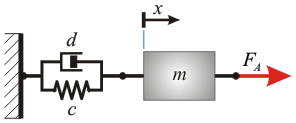
Bild 2: Beispielsystem „Einmassenschwinger“
Regelungstechnik (linear)
Erläuterung des Grundprinzips anhand eines einfachen Beispiels: Gemäß Bild 2 ist eine Masse $m$ über ein Feder-Dämpfer-Element mit der linearen Federkonstante $c$ sowie der linearen Dämpferkonstante $d$ inertial angekoppelt. Ein Messglied (Sensorik) misst die aktuelle Position $x$, während über eine Aktorik eine Kraft $F_A$ in das System eingeleitet werden kann. Es soll eine Positionsregelung mit vorgegebener Dynamik im Hinblick auf die Schnelligkeit und die Genauigkeit der Positionierung der Masse entworfen werden. Derartige Problemstellungen können bei linearen Systemen prinzipiell sowohl im ZEITBEREICH als auch im FREQUENZBEREICH gelöst werden.
Modellbildung ($\rightarrow$ Verhaltensmodell)
Nach NEWTON/EULER folgt für die Dynamik des Systems bzw. der Strecke:
\[m\ddot x = \sum\limits_{i = 1}^n {{F_i} = {F_A} - d\dot x - cx} \]
Für eine Analyse und Regelungssynthese im ZEITBEREICH lässt sich diese Differentialgleichung 2. Ordnung in die sogenannte Zustandsraumdarstellung $\underline {\dot x} = \underline A \underline x + \underline B \underline u$ überführen; mit den Zuständen $x$ (Position) und $\dot x = dx/dt = v$ (Geschwindigkeit):
\[\underbrace {\left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\ddot x} \end{array}} \right]}_{\underline {\dot x} } = \underbrace {\left[ {\begin{array}{*{20}{c}} 0&1\\ { - \frac{c}{m}}&{ - \frac{d}{m}} \end{array}} \right]}_{\underline A } \cdot \underbrace {\left[ {\begin{array}{*{20}{c}} x\\ {\dot x} \end{array}} \right]}_{\underline x } + \underbrace {\left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{m}} \end{array}} \right]}_{\underline B } \cdot \underbrace {\left[ {{F_A}} \right]}_{\underline u }\]
Alternativ können auch eine Analyse und Regelungssynthese im FREQUENZBEREICH erfolgen. Dazu wird auf die obige Differentialgleichung zunächst die LAPLACE-Transformation angewendet:
\[m{s^2}x\left( s \right) = {F_A}\left( s \right) - dsx\left( s \right) - cx\left( s \right)\]
Im Anschluss wird die Übertragungsfunktion $G\left( s \right)$ gebildet, welche die Beziehung zwischen Ein- und Ausgangsgröße(n) eines dynamischen Systems im FREQUENZBEREICH mathematisch beschreibt:
\[G\left( s \right) = \frac{{x\left( s \right)}}{{{F_A}\left( s \right)}} = \frac{1}{{m{s^2} + ds + c}}\]
Zustandsraumdarstellung und Übertragungsfunktion sind äquivalente Beschreibungen, bzw. im obigen Beispiel Modelle, desselben Systems. Je nach Art des zu regelnden Systems bzw. je nach Regelungsaufgabe ist das physikalisch-mathematische Modell in einer dieser Formen auszudrücken. Erst dann kann man die Methoden und Algorithmen der linearen Regelungstechnik anwenden, die zu einem großen Teil in Bild 4 dargestellt sind.
Das können wir für Sie tun
Das IMK deckt die gesamte Bandbreite der in Bild 4 dargestellten Bereiche ab und unterstützt Sie damit bei der Lösung Ihrer regelungstechnischen Aufgaben. Wichtige Konzepte/Methoden sind dabei bspw. die folgenden:
- Vorsteuerung
- Zwei-Freiheitsgrade-Struktur (siehe Bild 5)
Freiheitsgrad 1 $\rightarrow$ ①; Freiheitsgrad 2 $\rightarrow$ ② - Zustandsregler und Zustandsbeobachter (siehe Bild 6)
- Prädiktoren
- PI-Zustandsregler
- Störgrößenaufschaltung und Störgrößenbeobachter
- Zustandsapproximation bei Ausgangsrückführung
- ...
Ferner unterstützen wir Sie mit unseren umfangreichen Erfahrungen und Know-How im Bereich der Optimierung sowie der automatischen Adaption von Regelungen (Struktur und Parametrierung).
Bezogen auf die Referenzarchitektur des „Operator-Controller-Moduls“ (OCM) betreffen die hier vorgestellten Konzepte und Methoden überwiegend die Aufgaben des „Controllers“ und damit den „Motorischen Kreis“ (siehe Bild 5). Struktur und Parameter können im Rahmen einer (automatischen) Adaption generell umgeschaltet werden. Dies passiert jedoch auf den Operator-Ebenen (reflektorisch und kognitiv) des OCM und fällt damit dann in die Bereiche der nichtlinearen Regelungstechnik sowie der „Künstlichen Intelligenz“ (KI).
Zeitbereich, Frequenzbereich und LAPLACE-Transformation Sofern man das Verhalten eines dynamischen Systems (Regelkreis, Regelstrecke etc.) durch gewöhnliche Gleichungen und Differentialgleichungen beschreiben kann, deren Beziehungen untereinander linear und zeitinvariant sind, so kann man mittels der LAPLACE-Transformation die Differentialgleichungen im Zeitbereich in gewöhnliche Gleichungen im Frequenz- bzw. Bildbereich transformieren. Die „Problemlösung“ im Frequenzbereich gestaltet sich in vielen Fällen als deutlich einfacher. 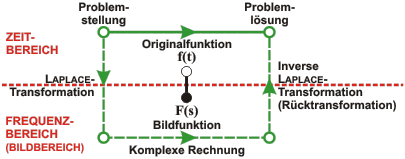 Bild 3: Die 2 Wege zur Problemlösung |
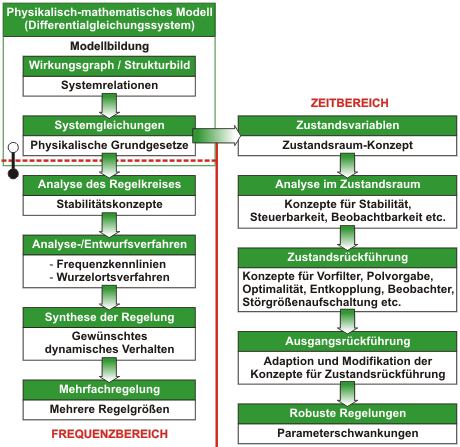
Bild 4: Grundgerüst der linearen Regelungstechnik am IMK
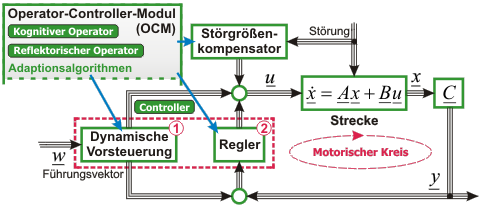
Bild 5: 2-Freiheitsgrade-Struktur mit Störgrößenkompensator und Adaption
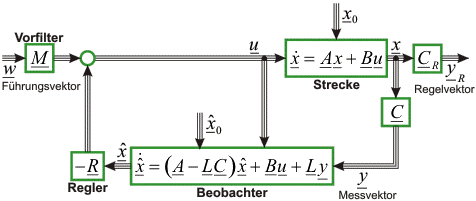
Bild 6: Zustandsregler mit Zustandsbeobachtung und Zustandsrückführung
(Beispiel 2: Der LUENBERGER-Beobachter)
Regelungstechnik (nichtlinear)
Im Bereich der nichtlinearen Regelungstechnik sehen wir sämtliche Methoden und Ansätze, die geeignet sind, nichtlineare Regelstrecken in gewünschter Weise zu beeinflussen. Die Methoden sind sehr vielfältig und können wiederum verschiedensten Kategorien zugeordnet werden. Sie reichen von der betriebspunktabhängigen Linearisierung in Verbindung mit „Gain-Scheduling“ über Fuzzy-Controller bis hin zu „Künstlichen Neuronalen Netzen“ (KNN), die dem Gebiet der „Künstlichen Intelligenz“ (KI) zuzurechnen sind. Einige wichtige und interessante Ansätze werden im Folgenden kurz aufgelistet; ohne Anspruch auf Vollständigkeit:
1. Regelungen für nichtlineare Regelstrecken
- Gain-Scheduling-Regler
- Reglerentwurf mittels exakter Linearisierung
- Das Backstepping-Verfahren
- Modellbasierte prädiktive Regelung
- Strukturvariable Regelungen mit Gleitzustand
- Fuzzy-Regelung
- Neuro-Regelung auf Basis „Künstlicher Neuronaler Netze“ (KNN)
- ...
- LUENBERGER-Beobachter für nichtlineare Regelkreise
- Beobachterentwurf mittels Linearisierung
- Das erweiterte KALMAN-Filter (EKF) für nichtlineare Systeme
- Neuronale Beobachter
- Lernfähige Beobachter
- ...
Künstliche Neuronale Netze (KNN) Durch die Integration von KNN sind bspw. die folgenden (neuen) Strukturen denkbar: Regelkreis mit ...
KNN eignen sich besonders gut für die Regelung nichtlinearer Systeme. Für die Adaption der KNN liegt das mathematische Modell des jeweiligen Systems idealerweise in der „Byrnes-Isidori-Normalform“ vor. 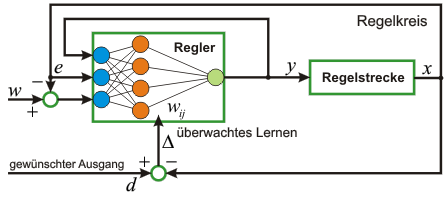 Bild 7: Regelkreis mit KNN als Zustandsregler |
Nichtlineare Regelungsnormalform Eine nichtlineare Regelstrecke sei in folgender Form gegeben: $\underline {\dot x} = \underline f \left( {\underline x } \right) + \underline g \left( {\underline x } \right) \cdot u$, $y = h\left( {\underline x } \right)$ Derartige Systeme lassen sich im Rahmen einer Koordinatentransformation $\underline x(t) \mapsto \underline z(t)$ in die sogenannte „Byrnes-Isidori-Normalform“ transformieren. Im Rahmen dieser Transformation wird der Zustandsvektor $\underline x(t)$ der Originaldarstellung in die Vektoren $\underline \alpha (t)$ und $\underline \beta (t)$ überführt, wobei ferner gilt: $\underline z \left( t \right) = \left[ {\begin{array}{*{20}{c}} {\underline \alpha \left( t \right)}\\ {\underline \beta \left( t \right)} \end{array}} \right]$ Die Vektoren $\underline \alpha (t)$ und $\underline \beta(t) $ besitzen folgende Eigenschaften:
Diese Art der Darstellung ist für die Analyse und die Synthese von nichtlinearen Regelungen deshalb von großer Bedeutung; sie bildet den Ausgangspunkt für viele Verfahren. |
„Fuzzy Logic“ Erst wenn man die einzelnen Teile eines Systems verknüpft, erschließt sich einem das „Ganze“ (s. a. Systemtheorie). Dann ist häufig nur ein Bruchteil der Daten nötig, um das System zu charakterisieren. Dies ist das Hauptprinzip der „Fuzzy Logic“ („Unscharfe Logik“) und der davon abgeleiteten „Fuzzy-Controller“. Durch „Unschärfe“ verschwinden die Grenzen zwischen den einzelnen Systemkomponenten, und das „Ganze“ wird sichtbar. | |||
| Frederic VESTER erklärt das Phänomen anhand des nebenstehend dargestellten Bildes: Erst wenn man es aus großer Entfernung betrachtet oder stark blinzelt, erkennt man den amerikanischen Präsidenten Abraham Lincoln. Fuzzy-Controller wenden genau dies Prinzip an. Sie basieren auf (sprachlich) „unscharf“ formulierten Aktionsregeln; exakte Messwerte werden nicht benötigt. | 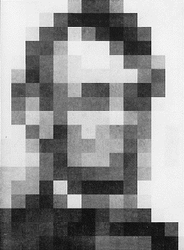 (Beispiel nach Frederic VESTER) | ||
Das können wir für Sie tun
In Abhängigkeit der Regelungsaufgabe bzw. des zu regelnden Systems (Regelstrecke) wählen wir ein geeignetes Verfahren aus und implementieren es auf einer Steuerung Ihrer Wahl.