Modellbildung & Simulation - IMK Engineering – Ingenieurbüro für Mechatronik und Kybernetik Dr. Bruns

Hauptmenü:

Kompetenzen

Kompetenzen ⇒ Modellbildung & Simulation

Einführung

Modelle sind Hilfsmittel beim Umgang mit der Realität. Ein Modell ist dabei eine vereinfachte Abbildung eines interessierenden Realitätsausschnitts; nur für diesen Ausschnitt soll es gültige Aussagen liefern. Problemstellungen und die daraus resultierenden Fragen, die es zu beantworten gilt, definieren den Modellzweck. Der Modellzweck wiederum ist die Grundlage für die richtige Wahl der Modellierungstiefe sowie der Modellierungsart.

Ein Roboter (reales System) kann bspw. durch ein CAD-Modell dargestellt werden. Dieses Modell enthält in der Regel Informationen zur Geometrie des Roboters (3D-Darstellung) sowie ggf. Informationen zu seinen Bewegungsmöglichkeiten im Sinne der Kinematik. Das CAD-Modell hat dabei vielleicht einfach nur den Zweck, dem Betrachter einen optischen Eindruck von dem realen System zu vermitteln, evtl. wird es auch für Bau- oder Arbeitsraumanalysen verwendet.

Derselbe Roboter kann aber auch durch ein Verhaltensmodell im Sinne der Dynamik bzw. der Kinetik beschrieben werden, das in der Regel in Form eines Differentialgleichungssystems vorliegt. Dieses Modell bzw. diese Form der Realitätsbeschreibung ist dann auf das dynamische Verhalten bzw. das Bewegungsverhalten des (realen) Systems „Roboter“ ausgerichtet.

Beide Modelle, CAD-Modell und Verhaltensmodell, beschreiben denselben Roboter, haben aber, wie oben beschrieben, unterschiedliche Modellzwecke und bilden deshalb auch unterschiedliche Realitätsausschnitte ab. Jedes Modell ist deshalb nur eine von vielen Möglichkeiten der Realitätsdarstellung.

Bevor weiter unten noch näher auf die Notwendigkeit sowie die Vorteile der Modellbildung und der Simulation eingegangen wird, soll zunächst anhand der folgenden Videos ein erster Eindruck davon vermittelt werden, was mit Modellen alles möglich ist (Video 1) und wie auf ihrer Basis ein reales System erfolgreich entsteht (Video 2).

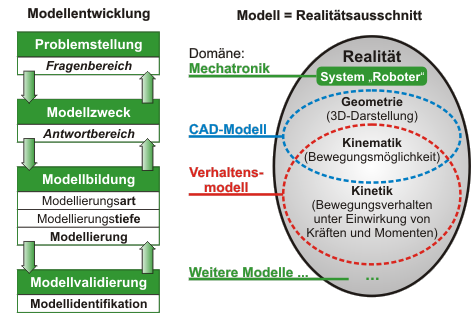
Bild 1: Modellentwicklungsprozess (links) und Modelldefinition (rechts)

Grundsatz erfolgreicher Modellbildung

Im Hinblick auf die Wahl der Modellierungstiefe sollte folgender Satz stets die Leitlinie sein:

„So genau wie nötig, so einfach wie möglich!“

Demnach beginnt man mit einem möglichst einfachen Modell bzw. mit einer möglichst geringen Modellierungstiefe. Erst wenn man feststellt, dass der geforderte Realitätsausschnitt nicht hinreichend genau beschrieben werden kann, erhöht man die Modellierungstiefe bzw. die Detaillierung.

Video 1: Modellbildung und Simulation (Disclaimer)

Video 2: Das modellbasiert realisierte System (Disclaimer)

TriPlanar (Anmerkung zu den Videos)

Die beiden oberen Videos zeigen den TriPlanar, eine parallelkinematische Handlingmaschine, die im Rahmen eines durch die DFG geförderten Forschungsvorhabens am Lehrstuhl für Automatisierungstechnik von Prof. Dr.-Ing. Joachim LÜCKEL entwickelt wurde. Zum TriPlanar sind zahlreiche Veröffentlichungen erschienen. Für nähere Informationen, insbesondere zur Entwurfsmethodik, empfehlen wir die Veröffentlichungen [1] und [2]. Weitere Informationen finden Sie unter Robotic Motion Control.

[1]	Kuhlbusch, Walter; Moritz, Wolfgang; Lückel, Joachim; Toepper, Stephanie; Scharfeld, Frank: TRIPLANAR – A New Process-Machine Type Developed by Means of the Mechatronic Design. 1999 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM ´99), Atlanta, GA, USA, 1999
[2]	Toepper, Stephanie; Kuhlbusch, Walter; Lückel, Joachim; Moritz, Wolfgang: Mechatronischer Entwurf der neuen Maschine TRIPLANAR für hochgenaue Fertigungs- und Messaufgaben. 44th International Scientific Colloquium, Technical University of Ilmenau, Ilmenau, 1999

––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Notwendigkeit und Vorteile der Modellbildung

Deshalb sind Verhaltensmodelle sehr wichtig und notwendig

Die Kybernetik („Die Kunst des Steuerns“) zielt darauf ab, dynamische Systeme in einer gewünschten Weise zu beeinflussen bzw. zu steuern. Falls es sich bei dem dynamischen System um ein mechanisches System handelt, wie etwa ein Roboter, so entspricht das dynamische Verhalten dem Bewegungsverhalten der mechanischen Struktur, und man spricht allgemein von Mechatronik anstatt von Kybernetik.

Das Verhalten eines technischen dynamischen Systems wird mit einer Informationsverarbeitung (Hardware und Software) beeinflusst, die im Allgemeinen eine Regelung (Feedback Control) enthält und damit eine Rückkopplung des zu kontrollierenden Systems benötigt. Alternativ hierzu ist auch eine reine Steuerung (Feedforward Control) möglich oder beides in Kombination (2-Freiheitsgrade-Struktur).

Um eine Regelung zu entwerfen, ist ein physikalisch-mathematisches Modell des zu regelnden Systems zwingend erforderlich. Ohne mathematisches Modell kann man weder eine geeignete Reglerstruktur bzw. einen geeigneten Algorithmus auswählen, noch weiß man, wie die entsprechenden Reglerparameter zu wählen sind. Ohne Modell bleibt nur ein „Trial-and-Error“-Verfahren, das am realen System durchzuführen ist. Dies ist sehr zeitaufwendig und führt in der Regel zu sehr suboptimalen Reglern und Reglerparametern. Weiterhin kann man mit „ungünstigen“ Reglerkonfigurationen großen Schaden am realen System anrichten, bis hin zur völligen Systemzerstörung.

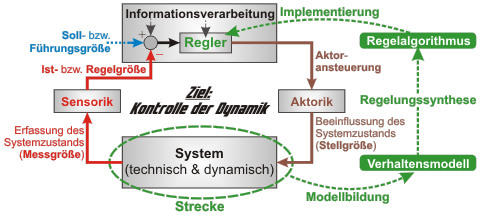
Bild 2: Prozess (grün) der Realisierung von Regelungen

Modellbildung und Systemtheorie

Das Ziel der „Allgemeinen Systemtheorie“ ist es, gemeinsame Wirkprinzipien und Gesetzmäßigkeiten in dynamischen Systemen zu finden und zu formalisieren, die domänenübergreifend angewendet werden können. Aus den gefundenen Analogien lassen sich dann „Modell-Module“ ableiten, die parallel bspw. für die Abbildung elektrotechnischer, mechanischer, strömungsmechanischer oder thermodynamischer Systeme verwendet werden können. (s. a. „Systemtheorie – Analogien“ sowie „Reduzierte Lösungselemente“ beim FEMS)

Die Vorteile von Modellbildung und Simulation

Unter „Simulation“ verstehen wir an dieser Stelle die Beschreibung des kontinuierlichen Verhaltens eines dynamischen Systems im Verlauf der Zeit. Dazu ist ein (physikalisch-mathematisches) Modell des jeweiligen Systems erforderlich, das in der Regel in Form eines Systems von Differentialgleichungen vorliegt. Vor der Simulation erfolgt also stets eine Modellbildung. Neben dieser Form der Simulation gibt es auch noch andere Formen bzw. Arten, die am IMK verwendet werden (s. a. „Operations Research – Stochastische Simulation“). Die wesentlichen Vorteile von Modellbildung in Kombination mit Simulation sind nebenstehend aufgelistet.

Ein lineares dynamisches System kann durch eine Zustandsdifferentialgleichung der folgenden Form beschrieben werden:

\[\underline {\dot x} \left( t \right) = \underline A \cdot \underline x \left( t \right) + \underline B \cdot \underline u \left( t \right)\]

Derartige Systeme lassen sich leicht mit Software-Tools wie Matlab (kommerziell) oder Scilab (Freeware) abbilden und analysieren. Darüber hinaus implementieren wir am IMK für Sie aber auch einen Simulationsalgorithmus auf Ihrem Echzeitsystem-System (PC oder MCU). Weshalb das manchmal sinnvoll und auch erforderlich ist, sehen Sie bspw. unter „Software“ und „Scientific Automation“.

Allgemeine Vorteile der Simulation:

Es kann unabhängig von der Art des betrachteten Systems mit einer einheitlichen Methodologie und Software gearbeitet werden.
Die Kosten der Modellbildung und der Simulation sind in der Regel nur ein Bruchteil dessen, was bei ähnlich umfassenden Untersuchungen an einem realen System entstehen würde.
Der zeitliche Ablauf des dynamischen Verhaltens kann bei der Simulation nahezu beliebig gerafft oder ausgedehnt werden, so dass genauere Beobachtungen möglich werden.
Eine Dynamik, die zur Systemzerstörung führen würde, bspw. aufgrund der Instabilität einer Regelung, hinterlässt am Computer keine Konsequenzen. Das reale System wird keinerlei Risiko unterzogen.
Die Auswirkungen von geplanten Systemänderungen können ohne nennenswerte Kosten innerhalb kürzester Zeit analysiert werden.
Anmerkung: So lassen sich bspw. auch durch „Trial-and-Error im Rechner“, also durch eine Vielzahl von Systemsimulationen mit variierenden Parametern, optimale Systemkonfigurationen finden. Ähnlich funktioniert auch die Identifikation von Modellparametern mittels (nichtlinearer) Optimierungsverfahren (s. a. Optimierung)
…

Unsere Kompetenzen

Unsere Kompetenzen liegen in der Modellierung dynamischer Systeme in einer Form, die in erster Linie den Entwurf von Regelungen ermöglicht. Die Regelungen dienen allgemein dem Zweck, die Systemdynamik zu kontrollieren bzw. in gewünschter Weise zu beeinflussen. Vielfach entsprechen diese Modelle dann physikalisch-mathematischen Verhaltensbeschreibungen in Form eines Differentialgleichungssystems. Dies muss aber nicht zwangsläufig so sein. In einigen Fällen ist es auch sinnvoll, mit „Black-Box“-Modellen zu arbeiten, die prinzipiell nicht an physikalische Parameter oder Strukturen des realen Systems gebunden sein müssen. In anderen Fällen ist es ebenfalls sinnvoll, mit „phänomenologischen“ Modellen zu arbeiten. Diese Modelle dienen hauptsächlich einer (stark) vereinfachten Beschreibung physikalischer Ursache-Wirkungs-Beziehungen, in Abhängigkeit physikalischer Parameter. Diese Art der Modelle kommt bspw. bei der Echtzeit-Simulation von Verbrennungsmotoren (s. a. Prozessregelung) zum Einsatz. Unser Know-How im Bereich der Modellbildung inkl. der Modellidentifikation (Bestimmung der Modellparameterwerte) und der Modellvalidierung (Validierung von Struktur und Parametern) ist umfassend. Wir stützen uns dabei unter anderem auf unsere Kenntnisse im Bereich der Systemtheorie sowie auf spezifisches und umfangreiches Wissen aus den Bereichen der nebenstehend dargestellten und physikalisch motivierten Domänen:

Mechanik: Diese Domäne beschäftigt sich mit der Bewegung von Körpern infolge wirkender Kräfte und Momente. Modellierungskenntnisse sind erforderlich, um mechanische Systeme jedweder Art beschreiben zu können. Dies wiederum ist Voraussetzung für „optimale Mechatronik“. (Einfaches Beispiel unter Regelungstechnik)
Strömungsmechanik: Diese Domäne wird auch als Fluidmechanik oder Strömungslehre bezeichnet und beschäftigt sich mit dem physikalischen Verhalten von Fluiden. Sowohl die Hydraulik als auch die Pneumatik werden von der Strömungsmechanik als Teilgebiete eingeschlossen.
Thermodynamik: Diese Domäne wird auch als Wärmelehre bezeichnet. Sie beschäftigt sich mit den unterschiedlichen Erscheinungsformen und Wandlungen von Energie, unter besonderer Berücksichtigung der Zustandsgrößen Volumen, Druck und vor allem der Temperatur.
Elektrotechnik: Insbesondere für die Modellierung von Sensoren und Aktuatoren sind Modellierungskenntnisse aus dieser Domäne erforderlich. Anschauliche Beispiele dazu finden Sie unter Funktionsorientierter Entwurf oder auch Optimierung.
Anmerkung: Auch in anderen Bereichen arbeiten wir mit „Modellen“, bspw. bei der Softwareentwicklung ($\rightarrow$UML). Die Ausführungen hier sollen auf rein physikalisch motivierte Modelle beschränkt bleiben.