Funktionsorientierter Entwurf - IMK Engineering – Ingenieurbüro für Mechatronik und Kybernetik Dr. Bruns
Hauptmenü:
Kompetenzen
Kompetenzen ⇒ Funktionsorientierter Entwurf (FEMS)
Bei den heute angewendeten Entwurfsmethoden stehen zumeist die Gestalt sowie die Gebrauchsfunktion des Produkts im Mittelpunkt, auch wenn es sich um ein mechatronisches Produkt handelt. Die Auslegung von Regelung und Steuerung erfolgt dann häufig erst in einer späten Phase des Entwurfsprozesses, vielfach auch nicht modellbasiert, sondern auf Basis von Erfahrungswerten und/oder in einem langwierigen „Trial-and-Error“-Verfahren. Der „Funktionsorientierte Entwurf mechatronischer Systeme“ (FEMS), wie er am Lehrstuhl für Automatisierungstechnik von Prof. Dr.-Ing. Joachim LÜCKEL vorwiegend in den 1990er Jahren entwickelt wurde, stellt die Bewegungsfunktion sowie deren frühzeitige Einbindung in den Entwicklungsprozess in den Mittelpunkt [2-5]. Dadurch wird das Leistungspotenzial eines Produktes sowohl hinsichtlich technischer als auch ökonomischer Eigenschaften (Zeit- und Kostenersparnis) signifikant verbessert:
- Kürzere Entwicklungszeiten und damit auch Reduktion der „Time-to-Market“ durch Einsparung von Entwicklungsschleifen.
- Beherrschung der zunehmenden Komplexität mechatronischer Systeme durch adäquate Strukturierungskonzepte.
- Optimierung von Gestalt und Gebrauchsfunktion im Hinblick auf Gewicht, verwendete Aktorik und Energieverbrauch durch längere Erhaltung der Entwurfsfreiheitsgrade (siehe Bild 1).
- Optimierung der Bewegungsfunktion im Hinblick auf Schnelligkeit und Genauigkeit durch Erweiterung der Entwurfsfreiheitsgrade.
- Aufdeckung von Synergien und neuen, nutzenmehrenden Funktionalitäten durch erweiterte Entwurfsfreiheitsgrade.
- Hervorragende Eignung für die horizontale und vertikale Integration im Sinne von „Industrie 4.0“ bei mechatronischen Produkten.
Übersicht der im Folgenden behandelten Themen:
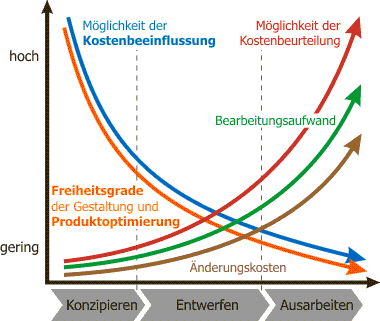
Bild 1: Kostenbeeinflussung vs. Kostenbeurteilung
| „Der Konstrukteur hat mit 60 bis 80 % der Kostenfestlegung eines Produktes eine hohe Kostenverantwortung im Unternehmen. Gerade die Phase des Konzipierens bietet die größten Möglichkeiten zur Kostenbeeinflussung. Es ist völlig sinnlos, erst im Nachhinein die Kosten zusammenzurechnen, wenn das Produkt schon gefertigt ist. Denn je weiter der Konstruktionsprozess fortgeschritten ist, desto geringer sind die Möglichkeiten, die Kosten zu beeinflussen. Notwendig ist eine Kostenfrüherkennung. Ein kurzer Regelkreis zwischen Konstruktion, Arbeitsvorbereitung und Kalkulation ist die Voraussetzung, um kostengünstig zu konstruieren.“ Erasmus Bode: Konstruktionsatlas, 1996 | ||
Zentrales Prinzip des FEMS
Begründung der Notwendigkeit
Bei mechatronischen Systemen müssen per Definition massebehaftete Körper bewegt bzw. deren Bewegungen nach definierten Kriterien beeinflusst werden. Die Masse der zu bewegenden Körper sowie die Leistung der Aktorik determinieren die Bewegungsfunktion. Wird die Bewegungsfunktion nicht frühzeitig in den Entwicklungsprozess einbezogen, so führt dies in der Regel zu einem suboptimalen Systemdesign, das sich dann bspw. in den folgenden Punkten zeigt:
- Die zu bewegenden Massen werden zu groß dimensioniert, folglich wird eine leistungsstärkere und damit meistens auch teurere Aktorik benötigt.
- Die Bewegungsfunktion ist suboptimal realisiert, das heißt geringere Schnelligkeit und/oder geringere Genauigkeit der Bewegung.
Weiterhin ist zu berücksichtigen, dass ohne ein Verhaltensmodell im Sinne eines physikalisch-mathematischen Modells des mechanischen Grundsystems keine (optimale) Auslegung der Regelung erfolgen kann (s. a. Modellbildung & Simulation sowie Regelungstechnik). Es bleibt dann nur das „Trial-and-Error“-Verfahren, das bei einem einfachen PID-Regler mit lediglich 3 Parametern schon als problematisch einzustufen ist.
Nicht zu unterschätzen sind auch die Synergieeffekte und zusätzlichen „Freiheitsgrade“ (siehe Bild 1), die aus einer frühzeitigen Einbeziehung des Zusammenspiels aller Systemkomponenten (Mechanik, Sensorik, Aktorik und Informationsverarbeitung) und aller beteiligten Fachdisziplinen (klassische Ingenieurwissenschaften, Elektronik, Informatik etc.) entstehen (Holismus).
Beispielsweise müssen die zu bewegenden Massen möglichst klein gehalten werden, wenn hohe Beschleunigungen erreicht werden sollen und/oder Material eingespart werden soll. Bei der Entwicklung von Robotern steht dies häufig im Gegensatz zu der Forderung nach möglichst hoher Steifigkeit des Systems. Die hohe Steifigkeit wurde häufig bzw. wird immer noch durch große Massen „erkauft“. Dadurch wurden Eigenfrequenzen des Systems erhöht und die Schwingungsamplituden reduziert. Dies sind Zielkonflikte, wie sie bspw. auch bei der Entwicklung passiver Fahrwerksysteme auftreten (s. a. Regelung aktiver Fahrwerksysteme, Konfliktdiagramm). Durch die ganzheitliche bzw. holistische Betrachtung ab Beginn des Entwicklungsprozesses sowie die Fokussierung auf die Bewegungsfunktion können diese Zielkonflikte gelöst oder zumindest signifikant abgemildert werden, wie auch dieses weitere Beispiel zeigt: Anfang der 1990er Jahre wurde am Lehrstuhl von Prof. LÜCKEL das Robotersystem TEMPO entwickelt [3], ein extrem leicht gebauter Roboter mit dementsprechend hohen Elastizitäten, aber dafür hohem Beschleunigungsvermögen. Das durch die hohen Elastizitäten induzierte Schwingungsverhalten wurde durch eine überlegene regelungstechnische Informationsverarbeitung (u. a. auf Basis eines Störgrößenkompensators und einer Ausgangsvektorrückführung) überkompensiert, so dass gegenüber seinerzeit handelsüblichen Robotersystemen eine um den Faktor 8-10 höhere Genauigkeit erreicht werden konnte [3].
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Die Kernelemente und Eigenschaften des FEMS
Der „Funktionsorientierte Entwurf mechatronischer Systeme“ (FEMS) setzt auf dem klassischen, konventionellen Entwurfsprozess nach Gerhard PAHL und Wolfgang BEITZ auf [1] (Bild 2, blaue Bereiche). Im Gegensatz zu einer Fokussierung auf die Gebrauchsfunktion stellt der FEMS jedoch die Bewegungsfunktion des Systems bzw. des Produkts in den Mittelpunkt. Dazu wird der konventionelle Entwurfsprozess in der frühen Phase um die sogenannte „Mechatronische Komposition“ erweitert (grüne Bereiche), die sich wiederum in die Phasen „Modellbildung“, „Analyse“ und „Synthese“ untergliedern lässt.
Die Bewegungsfunktion resultiert aus dem Zusammenspiel aller Komponenten (Mechanik, Sensorik, Aktorik und Informationsverarbeitung). Um die Bewegungsfunktion bereits in der frühen Entwurfsphase einbinden zu können, sich dabei aber nicht schon auf konkrete Elemente oder Baugruppen festlegen zu müssen, wird während der „Mechatronischen Komposition“ mit sogenannten „reduzierten Lösungselementen“ für alle beteiligten Komponenten gearbeitet. Es handelt sich dabei um Lösungselemente, die auf ihren wesentlichen Einfluss hinsichtlich des dynamischen Verhaltens des Gesamtsystems reduziert sind (Beispiel: Reduzierte Lösungselemente).
Eine Festlegung auf konkrete Elemente oder Baugruppen soll in der frühen Entwicklungsphase bewusst nicht erfolgen, um sich möglichst viele Entwurfsfreiheitsgrade noch zu erhalten, denn wie Bild 1 zeigt, können in dieser Phase die Kosten noch leicht beeinflusst und „optimiert“ werden. Gleiches gilt für das Produkt: Die Erhaltung der Entwurfsfreiheitsgrade ist elementar, um eine optimale Produktgestaltung zu erreichen und um langwierige und kostspielige Entwicklungsschleifen zu vermeiden. Anderenfalls können Lösungsprinzipien zu früh favorisiert oder ausgeschlossen werden, was im Nachhinein nur unter sehr hohem finanziellen und zeitlichen Aufwand korrigiert werden kann.
Die mechatronische Komposition umfasst die Integration heterogener Komponenten zu mechatronischen Systemen. Dies erfordert allerdings eine domänenübergreifende Kommunikation und Kooperation zwischen allen beteiligten Fachdisziplinen.
[1] | Pahl, Gerhard; Beitz, Wolfgang et al.: Konstruktionslehre – Methoden und Anwendung. Springer-Verlag, 1977-2013 | |
[2] | Lückel, Joachim; Jäker, Karl-Peter; Moritz, Wolfgang: Entwurfswerkzeuge der Mechatronik. FORUM ’90, Wissenschaft und Technik, Trier 1990 | |
[3] | Lückel, Joachim; Wittler, Gerd; Moritz, Wolfgang et al.: Funktionsorientierter Entwurf und Softwarewerkzeuge für mechatronische Systeme am Beispiel eines modularen Robotersystems. Fachtagung CAD '94, Paderborn, 17.-18. März 1994 | |
| [4] | Lückel, Joachim; Kuhlbusch, Walter; Moritz, Wolfgang; Toepper, Stefanie: Mechatronic Design of the New TriPlanar Machine for Highly Precise Process- and Measurement Tasks. In: 3rd Heinz Nixdorf Symposium on Mechatronics and Advanced Motion Control, Paderborn, 27.-28. Mai, 1999 | |
| [5] | Lückel, Joachim; Koch, Thorsten; Schmitz, Joachim: Mechatronik als integrative Basis für innovative Produkte. Mechatronik – Mechanisch/Elektrische Antriebstechnik, VDI-Berichte 1533, VDI-Verlag, Düsseldorf, 2000 | |
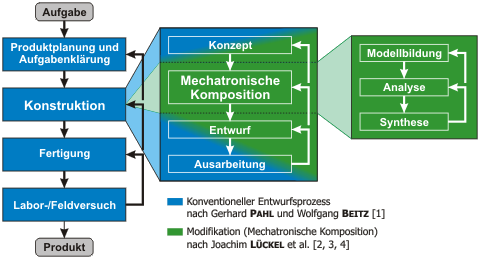
Bild 2: Entwurfsprozess für mechatronische Systeme (nach LÜCKEL et al. [2-5])
Die Mechatronische Komposition
Das Ziel der mechatronischen Komposition ist, das dynamische Bewegungs- und Systemverhalten des mechatronischen Gesamtsystems in den frühen Phasen des Entwurfsprozesses integriert zu entwerfen, zu analysieren und zu optimieren. Dies geschieht gemäß Bild 2 in den 3 folgenden Phasen:
- Modellbildung: In dieser Phase wird ein physikalisch-mathematisches Modell (mit reduzierten Lösungselementen) erstellt, mit dem das dynamische Verhalten des betrachteten Systems für den jeweiligen Zweck ausreichend genau beschrieben wird. Für die Wahl der Modellierungstiefe gilt: So genau wie nötig, so einfach wie möglich. Zu dieser Phase gehören auch zwingend die Schritte Identifikation bzw. Validierung des Modells (s. a. Modellbildung & Simulation)
- Analyse: Bei mechatronischen Systemen (die Phasen sind prinzipiell auf beliebige kybernetische Systeme übertragbar) werden mit Hilfe des Modells die Bewegungsmöglichkeiten und das (kontrollierte) Bewegungsverhalten analysiert. Dadurch können bspw. Fragen nach dem Arbeitsraum, nach den benötigten Kräften und Momenten (wichtig für die Dimensionierung der Aktorik) sowie nach dem Zeit- und Frequenzverhalten beantwortet werden. Ferner lassen sich Aussagen zu Stabilität bzw. Empfindlichkeit, Systemsteifigkeit und den Eigenschwingungsformen (Modalanalyse) treffen. Wichtig ist auch, dass nun direkt Aussagen zu Bauteilbelastungen getroffen werden können, bspw. in Form von auftretenden Kräften und Momenten, Drücken, mechanischen und elektrischen Spannungen etc.
- Synthese: Auf Basis der Analyseergebnisse wird das Systemverhalten verbessert und das Modell entsprechend angepasst. Über- oder Unterdimensionierungen bei mechanischer Grundstruktur und/oder Aktorik werden eliminiert. Die Informationsverarbeitung für Steuerung, Regelung und Überwachung wird entworfen oder angepasst und für das finale Modell optimiert. Die Phase der Synthese ist elementar für Einsparung von Kosten und Verkürzung der Entwicklungszeit bzw. der „Time-to-Market“.
Die Mechatronische Komposition wird „flankiert“ durch Ordnungs- und Strukturierungsmechanismen wie Modularisierung und Hierarchisierung. Dadurch wird die Komplexität mechatronischer Systeme, die nicht zuletzt aus den vielen beteiligten Fachdisziplinen bzw. Domänen resultiert, beherrschbar gemacht.
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Um Komplexität beherrschbar zu machen, sind in technischen Disziplinen, vor allem auch in der Informatik, schon frühzeitig Strukturierungskonzepte entstanden, die im Wesentlichen auf einer konsequenten Modularisierung und Hierarchisierung des Gesamtsystems aufbauen. Die weitverbreitete Verwendung von Bauteilhierarchien in der Konstruktionspraxis ist ein Beispiel für die Hierarchisierung. Im Bereich der Informatik „modularisiert“ bspw. die „Objektorientierte Programmierung“ (OOP) bestimmte Merkmale (Attribute) und Fähigkeiten (Methoden) einer Software-Komponente in Form von „Klassen“. Aus einer Klasse können mehrere Objekte „instanziiert“ werden (Wiederverwendbarkeit), die sich im Wesentlichen durch unterschiedliche Ausprägungen ihrer Attribute (Zuweisung konkreter Werte) unterscheiden.
Diese Ansätze können sehr gut auf den Entwurfsprozess mechatronischer Systeme bzw. Produkte übertragen werden. Dazu müssen die unterschiedlichen und zum Teil auch fachspezifischen Bauteile oder Baugruppen, inkl. der Software bzw. der Informationsverarbeitung, als Basiselemente im Sinne von Modulen mit standardisierten Schnittstellen definiert werden. Im Anschluss können dann mit diesen Modulen komplexe und hierarchisch aufgebaute mechatronische Systeme gebildet werden („Bottom-Up“-Vorgehen).
Bei der Entwicklung neuer Systeme oder Produkte erfolgt nach Formulierung eines Lastenhefts meistens die Definition der Funktionsstruktur (vgl. [1]). Dabei wird nach der klassischen Konstruktionslehre die Gebrauchs- oder auch Gesamtgebrauchsfunktion hierarchisch untergliedert in Teilgebrauchsfunktionen, die durch reale Baugruppen oder Aggregate zu realisieren sind. Der „Funktionsorientierte Entwurf mechatronischer Systeme“ (FEMS) baut auf dieser Praxis auf und ordnet darüber hinaus der Funktionsstruktur bzw. Funktionshierarchie auch noch Bewegungsfunktionen zu, die mit „reduzierten Lösungselementen“ realisiert werden („Top-Down“-Vorgehen).
Der Entwurfsprozess mechatronischer Systeme gestaltet sich häufig als ein Wechselspiel zwischen „Bottom-Up“- und „Top-Down“-Vorgehen.
Im Rahmen des FEMS sind Strukturierungselemente entstanden, welche die Modularisierung und die Hierarchisierung der Funktionsstruktur im Sinne der Bewegungsfunktion unterstützen. Dabei handelt es sich um das „Mechatronische Funktionsmodul“ (MFM), die „Mechatronische Funktionsgruppe“ (MFG), das „Autonome Mechatronische System“ (AMS) und das „Vernetzte Mechatronische System“ (VMS).
Viele Elemente des FEMS sind 2002 in die VDI-Richtlinie 2206 „Entwicklungsmethodik für mechatronische Systeme“ eingeflossen. | ||
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
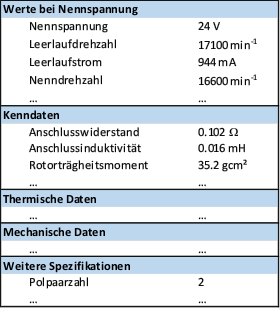
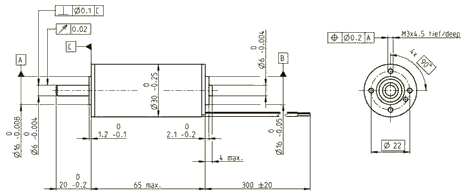
Die „Reduzierten Lösungselemente“ werden für die „Mechatronische Komposition“ benötigt. Sie haben nicht zum Ziel, die konventionellen Lösungselemente (Maschinenelemente, Bauteile oder Baugruppen) mit ihren gestalt- und gebrauchsorientierten Beschreibungen (Tabelle unten, linke Spalte) zu ersetzen. Vielmehr sollen diese Beschreibungen auf den für die Untersuchung dynamischer Systeme relevanten Anteil reduziert werden, sofern die dynamisch relevanten Informationen vorhanden sind. Falls sie nicht vorhanden sind, was häufig der Fall ist (Tabelle unten, rechte Spalte), dann soll die bisherige Beschreibung des Lösungselements um diese Informationen ergänzt werden.
Wie in der Elektrotechnik/Elektronik gibt es auch hier passive und aktive Komponenten oder Bauteile. Ein Beispiel für eine aktive Komponente ist der elektromechanische Aktor (DC-Motor), der in der unten folgenden Tabelle dargestellt ist. Eine passive Komponente ist bspw. ein simpler Torsionsstab, der innerhalb eines mechatronischen Systems zyklisch wechselnden Belastungen ausgesetzt ist. Die wesentliche Information für die Abbildung des Torsionsstabs als reduziertes Lösungselement entspricht dann seiner Drehsteifigkeit [Nm/rad].
Durch den Transformationsvorgang von konventionellen Lösungselementen zu reduzierten Lösungselementen wird eine Abstraktion vorgenommen, die auf die prinzipielle Struktur des dynamischen Verhaltens führt. Mit dieser Struktur können viele ähnliche, tatsächliche bzw. reale Lösungselemente beschrieben werden. So können bspw. mit dem unten dargestellten Differentialgleichungssystem (Tabelle, rechte Spalte) eine Vielzahl von DC-Motoren hinsichtlich ihrer Dynamik beschrieben und simuliert werden. Voraussetzung dafür ist eine an das reale Lösungselement gekoppelte Parametrierung, im unten stehenden Beispiel also eine Belegung der Parameter $R_A$, $L_A$, $k_M$, $J_M$ und $d$ mit konkreten Werten.
Spätestens an dieser Stelle werden die Analogien zu bzw. Gemeinsamkeiten mit der „Objektorientierten Programmierung“ (OOP) deutlich (s. o.: Strukturierungsmechanismen). Die Parameter der reduzierten Lösungselemente entsprechen den Attributen der OOP; die dynamischen Struktureigenschaften kann man mit den Methoden vergleichen. Ein nicht-parametriertes, reduziertes Lösungselement entspricht dann prinzipiell einer Klasse der OOP, während ein parametriertes Lösungselement einer Instanz dieser Klasse, also einem Objekt entspricht. Vor dem Hintergrund der reduzierten Lösungselemente kann man also auch von „Lösungsklassen“ und „Lösungsobjekten“ sprechen und sich in diesem Sinne weitere Ansätze aus dem Bereich der OOP (Vererbung, Polymorphie etc.) für die Entwicklung mechatronischer Systeme zu Nutze machen! Davon macht das IMK auch Gebrauch.
| Im Zuge von Industrie 4.0 erhalten die „Reduzierten Lösungselemente“ eine besondere Bedeutung, da sie Voraussetzung sind für eine effiziente horizontale Integration entlang der Wertschöpfungskette eines mechatronischen Produkts. Neben den gebrauchs- und gestaltorientierten Informationen (Tabelle unten, links) sollten die dynamischen Eigenschaften der reduzierten Lösungselemente (Tabelle unten, rechts) mit in die Beschreibung von Komponenten mechatronischer Produkte aufgenommen werden. Ist diese Beschreibung dann noch in standardisierter Form (bspw. eCl@ss, AutomationML etc.) online zu jeder Zeit an jedem Ort verfügbar, so sind die Voraussetzungen für unternehmensübergreifendes „Engineering“ mechatronischer Produkte prinzipiell erfüllt. | ||
| Lösungselement: Elektromechanischer Aktor (DC-Motor) | |
| Gebrauchsfunktion (gestaltorientiert) | Bewegungsfunktion (Reduziertes Lösungselement) |
   | Ersatzschaltbild 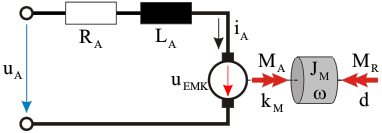 Differentialgleichungen \[{u_A} = {R_A} \cdot {i_A} + {L_A} \cdot \frac{{d{i_A}}}{{dt}} + {u_{EMK}},\;\;\;\;u_{EMK}=k_M \cdot \omega\] \[{J_M} \cdot \dot \omega = {M_A} - {M_R} = {k_M} \cdot {i_A} - d \cdot \omega \] Zustandsraumdarstellung \[\left[ {\begin{array}{*{20}{c}} {\frac{{d{i_A}}}{{dt}}}\\ {\dot \omega } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_A}}}{{{L_A}}}}&{ - \frac{{{k_M}}}{{{L_A}}}}\\ {\frac{{{k_M}}}{{{J_M}}}}&{ - \frac{d}{{{J_M}}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{i_A}}\\ \omega \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_A}}}}\\ 0 \end{array}} \right] \cdot {u_A}\] System- bzw. Zustandsgrößen
Parameter des Systems
|